跳转至

树状数组

用途

以 \(O(log(n))\) 计算区间和 支持单点修改

核心算法

维护树状数组，使其序号为 i 的数，存储的正好就是原数组中长度为 lowbit(i) 且以 i 结尾的序列的和

计算lowbit ( int x )

lowbit是树状数组的核心

它的本质是：求 x 的二进制的末尾的0个数，这恰好是以第 x 个数为结尾的区间，所管辖的长度

1
2
3
int lowbit(cint& x){
    return  x & (-x);
}

e.g. 14

正码：1110

反码：0001

补码：0010

（负数用补码表示，补码=反码加1）

重要注意点（修改与查询的核心）

  1. 两个数组，下标序号都从1开始
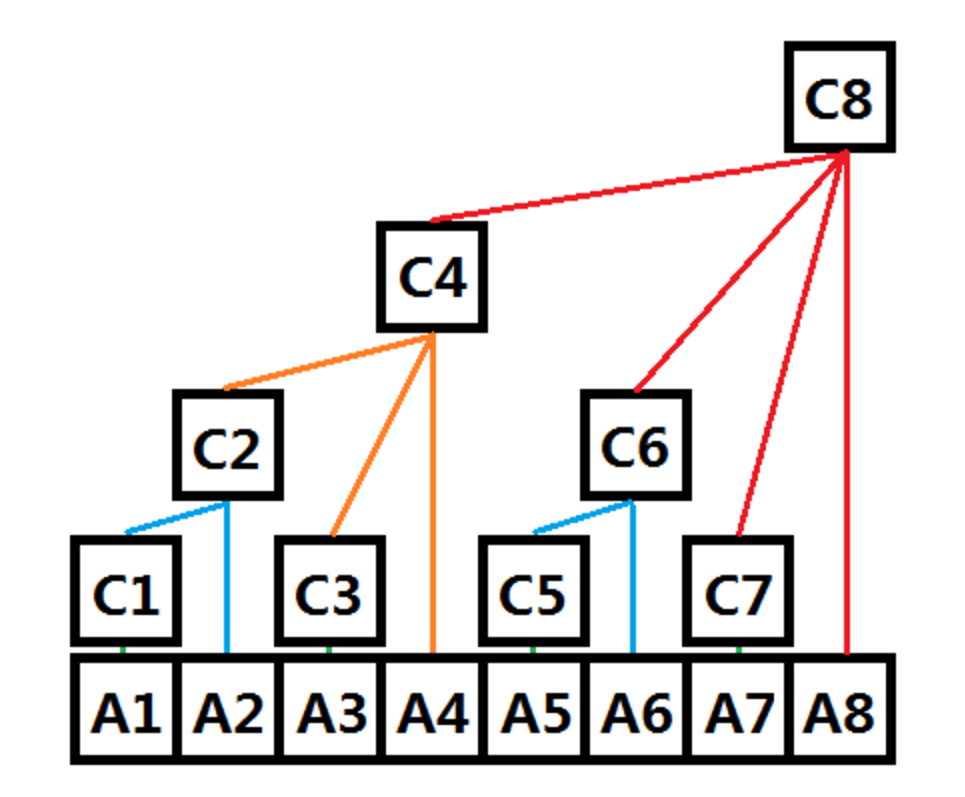
  2. 在树状数组中，序号为 i 的数表示原数组中长度为 lowbit(i) 且以 i 结尾的序列（亦称作序列 i ）的和。
  3. 在树状数组中，i + lowbit(i) 为序列 i 的父亲序列；i - lowbit(i) 为最近的兄弟序列（如 c7 -> c6 -> c4）
  4. 根据上一条，我们用 i + lowbit(i) 维护修改操作；
  5. 用 i - lowbit(i) 进行查询操作（一直减到 0 即可遍历所有子序列）
  6. 树状数组只能用于查询前缀和，查询单点（或区间）作差即可

enter image description here

修改查询代码实现（单点修改 区间查询）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
int sum_up(int p) { // 以log计算前缀和
    int cnt = 0;
    while (p) {
        cnt += t_nums[p];
        p -= lowbit(p);
    }
    return cnt;
}

// 在p位置上加上value
void add(int p, int value) {
    while (p <= len) {
        t_nums[p] += value;
        p += lowbit(p);
    }
}

初值可以直接使用add(pos,val)进行修改

【五分钟丝滑动画讲解 | 树状数组】 【精准空降到 04:00】

典型应用

单点修改 区间查询

这就是板子
查询两次分别得到 1~L-1 和 1~R的和

区间修改 单点查询

差分数组的初值 t[i] = a[i] - a[i-1]

求单点即为求区间和 [1,n]，也即 sum_up(n)

修改时，我们只用修改区间端点

修改区间 [a,b] 时有：

B[a]+=k；B[b]-=k；

区间修改 区间查询

一维树状数组——区间修改区间查询.png

维护两个树状数组，按公式计算即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
ll t[maxn], ti[maxn];
void add(int pos, ll val) {
    for (int i = pos; i <= n; i += lowbit(i)) {
        t[i] += val;
        ti[i] += val * pos;
    }
}

ll qry(int pos) {
    ll cnt = 0;
    for (int i = pos; i; i -= lowbit(i)) { cnt += (pos + 1) * t[i] - ti[i]; }
    return cnt;
}

void modify(int l, int r, ll x) {
    add(l, x), add(r + 1, -x); //差分维护
}

二维树状数组

二维树状数组

区查区改

上帝造题的七分钟

输入数据的第一行为 X n m，代表矩阵大小为 \(n\times m\)。
从输入数据的第二行开始到文件尾的每一行会出现以下两种操作：
- L a b c d delta —— 代表将 \((a,b),(c,d)\) 为顶点的矩形区域内的所有数字加上 \(delta\)。
- k a b c d —— 代表求 \((a,b),(c,d)\) 为顶点的矩形区域内所有数字的和。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
inline int lowbit(cint& p) { return p & (-p); }

int N, M; ///别忘了赋值

struct TreeArray_2D_Diff {
    int ori[maxn][maxn], ori_x[maxn][maxn], ori_y[maxn][maxn],
        ori_x_y[maxn][maxn];

    void add(int posx, int posy, int value) {
        for (int i = posx; i <= N; i += lowbit(i)) {
            for (int j = posy; j <= M; j += lowbit(j)) {
                ori[i][j] += value;
                ori_x[i][j] += value * posx;
                ori_y[i][j] += value * posy;
                ori_x_y[i][j] += value * posx * posy;
            }
        }
    }
    // 一并维护四个数组！

    // 左上角的矩阵和 计算子矩阵还要再处理
    int sum(int posx, int posy) {
        int cnt = 0;
        for (int i = posx; i; i -= lowbit(i)) {
            for (int j = posy; j; j -= lowbit(j))
                cnt += (posx + 1) * (posy + 1) * ori[i][j]
                       - (posx + 1) * ori_y[i][j] - (posy + 1) * ori_x[i][j]
                       + ori_x_y[i][j];
            // 注意：这里是齐次的四个式子 xy别搞反
        }
        return cnt;
    }

    void range_add(int a, int b, int c, int d, int delta) {
        add(a, b, delta);
        add(c + 1, d + 1, delta);
        add(a, d + 1, -delta);
        add(c + 1, b, -delta);
        // 较大的点坐标要加一
    }
} pic;

// 区间修改区间查询 二维树状数组模板
// 要开四个 用公式维护

int main() {
    ios::sync_with_stdio(0);
    char op;
    cin >> op >> N >> M;
    while (cin >> op) {
        int a, b, c, d, delta;
        cin >> a >> b >> c >> d;
        if (op == 'L') {
            cin >> delta;
            pic.range_add(a, b, c, d, delta);
        } else {
            cout << pic.sum(c, d) - pic.sum(a - 1, d)
            - pic.sum(c, b - 1)+ pic.sum(a - 1, b - 1)
                 << endl;
        }
    }

    return 0;
}

求区间最值（建议还是用线段树 好写又好调）

树状数组求区间最值_UniverseofHK的博客-CSDN博客_树状数组求区间最值

单点修改

对于单点修改，不能只比较更新父节点的区间最值，因为树状数组序号为x的数代表的是一个区间的最值，因此要先比较子区间的最值后，才能继续向上传递。

让 x 不停减去 $ 2^k $，把所有能转移过来的子区间更新：

QQ截图20230219150453.png

显然，这个 x 可以由这四个子区间转移而来，再和 a[x] 比较取max

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
void updata(int x) {
    while(x<=N) {
        b[x]=a[x]; // 先用自己修改自己
        int lx=lowbit(x); // lx为[x-lowbit(x)+1, x]的区间长度
        for(int i=1; i<lx; i<<=1) {
            b[x]=max(b[x],b[x-i]);
        }
        x+=lowbit(x);
    }
}

区间查询最值

以最大值为例：

当y-lowbit(y)>=x时，[x, y]区间包含了[y-lowbit(y)+1, y]区间，因此可以直接使用树状数组这个区间的最值（即b[y]）:

当y-lowbit(y)<x时，上述包含关系不成立，因此只能先委屈的使用原数组a[y]的值，然后将y减1；直到满足上述条件（或结束）:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
int query(int x, int y) {
    int ans=0;
    while(y>=x) {
        ans=max(ans,a[y]), --y;
        while(y-lowbit(y)>=x) {
            ans=max(ans,b[y]);
            y-=lowbit(y);
        }
    }
    return ans;
}