AGC031D A Sequence of Permutations
我们尝试用代数的语言建模:
假设初始排列为\(a_0=1,2,\cdots,n\)。我们想要只通过一次变换得到答案排列,现在求出这样一个变换。
对于前两个,设\(P,Q\)为置换,记作:
\[
P=\begin{pmatrix}1,2,\cdots,n\\ p_1,p_2,\cdots,p_n\end{pmatrix},Q=\begin{pmatrix}1,2,\cdots,n\\ q_1,q_2,\cdots,q_n\end{pmatrix}
\]
这类似一对一的函数,上面的值为\(x\),下面的值为其对应的\(y\)。可以用数组实现,上面一行看成是下标。
则\(a_0\)每个元素通过这两个置换:
\(P(a_0) = a_1,Q(a_0)=a_2\)
排列\(f(p,q)\)也可以看成一个置换,而且有:
\[
F=\begin{pmatrix} p_1,p_2,\cdots,p_n \\ q_1,q_2,\cdots,q_n \end{pmatrix}
\]
为什么呢?我们不妨举个例子:
\[
P=\begin{pmatrix}1,2,3,4\\ 3,1,4,2\end{pmatrix},Q=\begin{pmatrix}1,2,3,4\\ 4,3,1,2\end{pmatrix}
\]
根据题意,可以推出\(a_3=3,2,4,1\),则
\[
F=\begin{pmatrix}1,2,3,4\\ 3,2,4,1\end{pmatrix}
\]
仔细观察一下这个对应关系,1->3,2->2,3->4...,不就是第\(p_i\)个数对应\(q_i\),然后再按\(p_i\)顺序写出吗?
由此,我们有\(F(P(a_0))=Q(a_0)\),不妨引入一个记号 \(\circ\) 复合一下置换运算:\(F \circ P = Q\)
不难发现,在这个代数系统中,满足结合律,存在逆元和单位元。但不满足交换律!!!
注:单位元为\(e=\begin{pmatrix}1,2,\cdots,n\\ 1,2,\cdots,n\end{pmatrix}\)。求逆上下翻转即可。
并且有:\((p \circ q)^{-1} = q^{-1}\circ p^{-1}\)(要换位)
等式两边同时复合\(P\)的逆\(P^{-1}\),有\(F = Q \circ P^{-1}\)
多算几步:
\[
\begin{gathered}
a_1=p \\
a_2=q \\
a_3=q\circ p^{-1} \\
a_4=q\circ p^{-1}\circ q^{-1} \\
a_5=q\circ p^{-1}\circ q^{-1}\circ p\circ q^{-1} \\
a_6=q\circ p^{-1}\circ q^{-1}\circ p\circ p\circ q^{-1} \\
\end{gathered}
\]
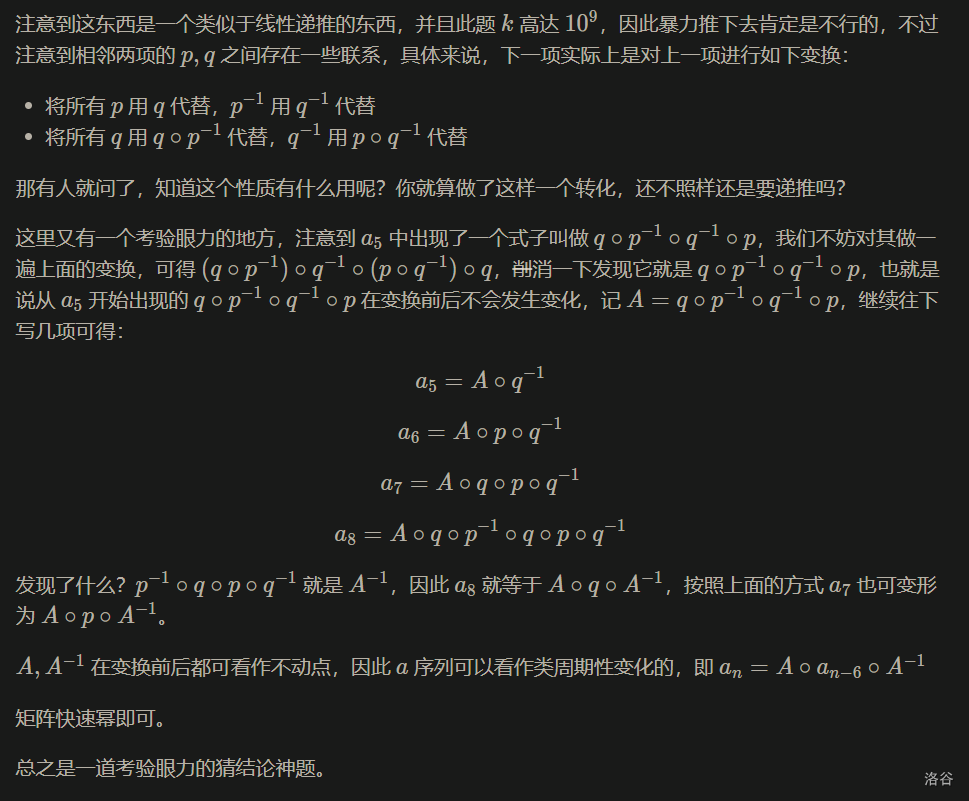
规律已经很显然了,这个序列以6为周期,每6项就会在两边分别乘上一个\(A\)和\(A^{-1}\),求出个数快速幂即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 | #include <bits/stdc++.h>
using std::cin;
using std::cout;
using LL = long long;
const int maxn = 1e5+10;
int n,k;
struct Perm{
int a[maxn];
Perm(){
for(int i=1;i<=n;i++) a[i]=i;
}// 1,2,...,n
// 复合运算 a*b = a(b())
Perm operator *(const Perm &b) const{
Perm ans;
for(int i=1;i<=n;i++){
ans.a[i] = a[b.a[i]];
// 跟矩阵快速幂不太一样~
}
return ans;
}
}p,q;
// 求逆
Perm inv(const Perm &x){
Perm ans;
for(int i=1;i<=n;i++){
ans.a[x.a[i]] = i;
}
return ans;
}
// 快速幂 求A和A的逆的幂
Perm qpow(Perm x,int e){
Perm ans;
while(e){
if(e&1) ans=ans*x;
e>>=1,x=x*x;
}
return ans;
}
int main(){
cin >> n >> k;
for(int i=1;i<=n;i++)
cin >> p.a[i];
for(int i=1;i<=n;i++)
cin >> q.a[i];
k--;
Perm ans,A=q*inv(p)*inv(q)*p;
switch (k%6){
case 0: ans=p;break;
case 1: ans=q;break;
case 2: ans=q*inv(p);break;
case 3: ans=A*inv(p);break;
case 4: ans=A*inv(q);break;
case 5: ans=A*p*inv(q);break;
}
ans=qpow(A,k/6)*ans*qpow(inv(A),k/6);
for(int i=1;i<=n;i++) cout << ans.a[i] << ' ';
return 0;
}
|
