从gcd到exgcd

注：如果方程设成ax-by=0之类的，判断-b即可。详见本文。

Part 0 前言

gcd以及exgcd算法是oi数论的基础，不管是求逆、解不定方程还是扩展中国剩余定理等都需要用到这里的知识。

---

Part 1 引入——求解gcd

欧几里得算法

我们_{~小学二年级}~就学过最大公约数，并了解过一种计算gcd的方法——辗转相除法。其定义如下：

int gcd(int a,int b){
    if(b==0) return a;
    return gcd(b,a%b);
}

该算法用到了一个重要的性质：

$gcd(a,b) = gcd(b,a\bmod b)$

笔者太菜，有关证明详见 OI-wiki-最大公约数

而exgcd，便是以这段代码为基础，转化而来。它可以求解形如$ax+by=c$的方程（整数域中）。我们先学习一下怎样判断其无解。

---

裴蜀定理

设 $a,b$ 是不全为零的整数，则存在整数$x,y$，使得 $ax+by=gcd(a,b)$

这句话告诉我们什么道理呢？

1. $ax+by=c$ 这个方程有整数解，当且仅当 $gcd(a,b)|c$
2. 令$f=ax+by$，在整数域中，使得 $f>0$ 且 $f$ 尽可能的小，则$f_{min}=gcd(a,b)$

对于多元有推论：

1. n元一次线性方程 $\sum\limits_{i=1}^nA_i\times X_i=C$有整数解，当且仅当 $gcd(A_1,A_2,...,A_n)|C$
2. 在整数域中，使得 $C>0$ 且 $C$ 尽可能的小，则$C=gcd(A_1,A_2,...,A_n)$

当你学会这个推论，那么便可以解决这道题了：

P4549 【模板】裴蜀定理

---

Part 2 推导

exgcd算法

别被标题吓到，其实这个挺简单的。 学会推式子，不会忘了咋打_~

注意：标准的 exgcd 只能用于求解方程$ax+by=gcd(a,b)$，若$c$是$gcd(a,b)$的倍数，我们在后文讨论。

如题，我们有$ax+by=gcd(a,b)$

考虑进行一次迭代，带入$a=b,b=a\%b$，我们又有：$bx'+(a\%b)y'=gcd(b,a\%b)$

注意这里的$x',y'$系数已经改变，新方程的解与原方程$x,y$不一样，故另作标号。

类似gcd，exgcd经过不断迭代递归，最后也会到达状态为exgcd(a,0)的形式，即y系数为0，x系数为a，方程为$ax+0y=gcd(a,0)=a$，故此时$x=1,y=0$

那么如何通过这个解求得上一个方程的$x,y$？

---

我们知道，$gcd(a,b) = gcd(b,a\%b)$ ，所以 $ax+by=bx'+(a\%b)y'$

又$a\%b=a-b*\left \lfloor a/b \right \rfloor$，所以有：

$ax+by$

$=bx'+(a-b*\left \lfloor a/b \right \rfloor)y'$

$=bx'+ay'-b*\left \lfloor a/b \right \rfloor y'$

$=ay'+b(x'-\left \lfloor a/b \right \rfloor y')$

待定系数，我们有$x=y',y=x'-\left \lfloor a/b \right \rfloor y'$

由此，我们便可以一层一层向上推出原方程的一组解。

代码如下：

LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL px, py; // 上一次的答案(x'和y')
    LL ans = exgcd(b, a % b, px, py);
    x = py, y = px - a / b * py;
    return ans;
}

这里可以直接在exgcd中求得gcd(a,b)的值，但是若传入的参数a,b为负数，则gcd有可能是负数。

---

推导通解

那么已知一组特解$(x_0,y_0)$，如何才能求出方程的通解呢？或者限定$x$或$y$的值为最小正整数，该如何求解？下面是通解的推导：

$ax_0+by_0=gcd(a,b)$

$\Rightarrow ax_0+k*lcm(a,b)+b_y0-k*lcm(a,b)=gcd(a,b)$

我们知道$lcm(a,b)=ab/gcd(a,b)$，故上式可化为：

$ax_0+a(k*b/gcd)+by_0-b(k*a/gcd)=gcd(a,b)$

$\Rightarrow a(x_0+k*b/gcd)+b(y_0-k*a/gcd)=gcd(a,b)$

待定系数得：$\begin{cases} x=x_0+k*b/gcd \\ y=y_0-k*a/gcd \end{cases}$

由此，我们便有了求解$x$或$y$的最小正整数解的方法：

注意到式子形如$x=a+kb$，也即$x \equiv x_0 \pmod{b/gcd}$（这对于y也同理）

设$p=\left|b/gcd\right|$，则x的最小整数解即为$x = (x_0 * gcd \% p + p) \% p$

---

更一般的情况

上一节推导了$ax+by=gcd(a,b)$的通解，而一般往往求解的方程是$ax+by=c=n*gcd(a,b)$

聪明的你会说，给算出来的x和y乘个n不就得了，即：

$\begin{cases} x'=nx=n*(x_0+k*b/gcd) \\ y'=ny=n*(y_0-k*a/gcd) \end{cases}$

但是，如果你直接给上一节算出的最小整数解乘n，其实不一定是该方程的最小整数解：

$$\begin{cases} x'=nx_0+kn*b/gcd \rightarrow nx_0+q*b/gcd \\ y'=ny_0-kn*a/gcd \rightarrow ny_0-q*a/gcd \\ \end{cases}$$

在构造$x'$和$y'$时，我们只要求$kn$是整数，故$k$实际上可以取任意实数，可以一并视为一个倍数$q$。

从集合的角度看，其实下面这组解集是包含上面那组解集的。

我们不难得到最小整数解：

$x' = (x_0 * (c/gcd) \% p + p) \% p$，其中$p=\left|b/gcd\right|$

---

那如果$a,b$有负数呢？我们不妨假设$a>0,b>0$：

$-ax+by=n*gcd(a,b)$

我们有$a(-x/n)+b(y/n)=gcd(a,b)$，说明exgcd求得的特解$x_0=-x/n,y_0=y/n$，移项解出$x$或$y$，再利用取模的公式即可（下文有图像）。

代码实现

#include <cmath>
// 求解形如ax+by=0
// 若形如ax-by=0，系数变为a,-b

LL a, b, c, X0, Y0;
LL gcd = exgcd(abs(a), abs(b), X0, Y0); // gcd一定要是正值
if (c % gcd != 0) continue;             // 先判方程无解
LL p = abs(b / gcd);
if (a < 0) X0 = -X0;                    // 系数为负 解也为负
// if (b < 0) Y0 = -Y0;

// 取决于要取哪个值，算一个带入求另一个即可
LL x = (X0 * c / gcd % p + p) % p;
LL y = (c - a * x) / b;

Part 3 几何意义与一些问题

裴蜀定理到底说了个啥？为啥取模求最小正整数的方法对于所有情况都适用？

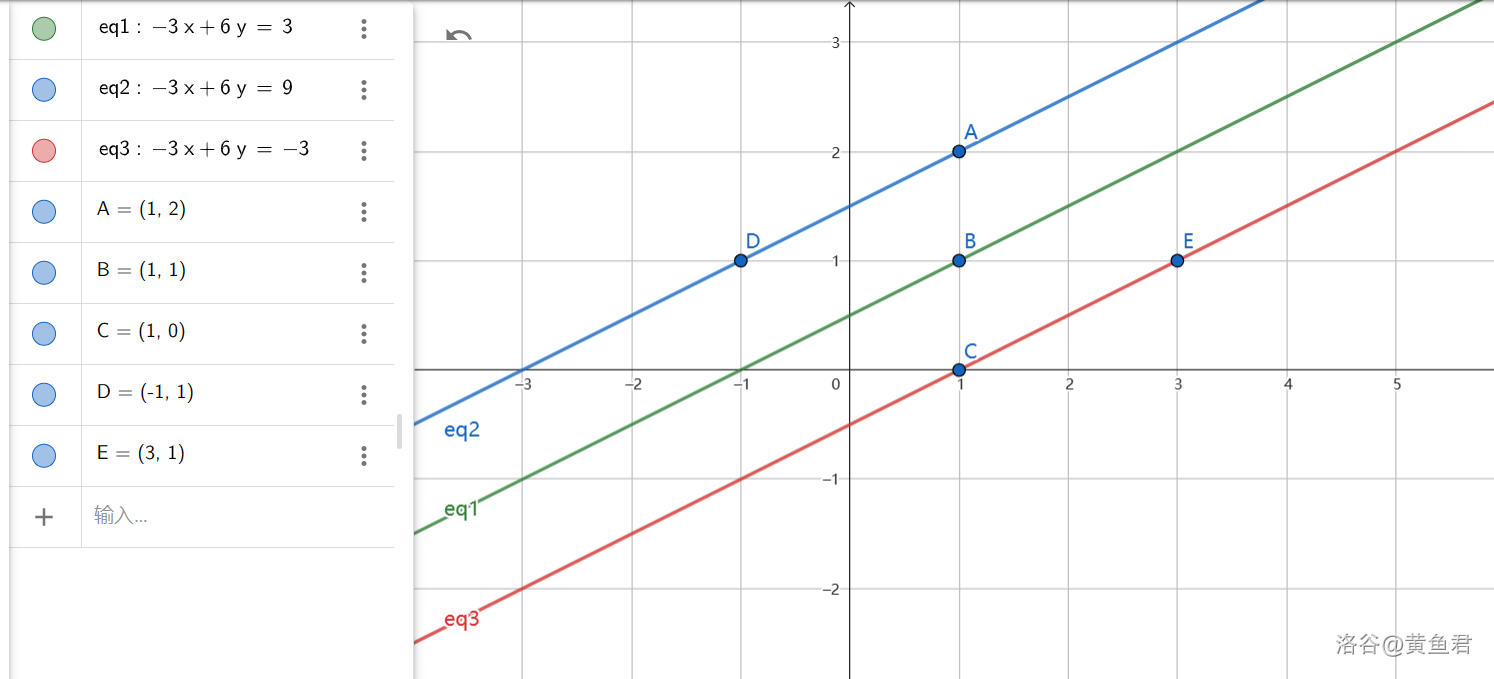
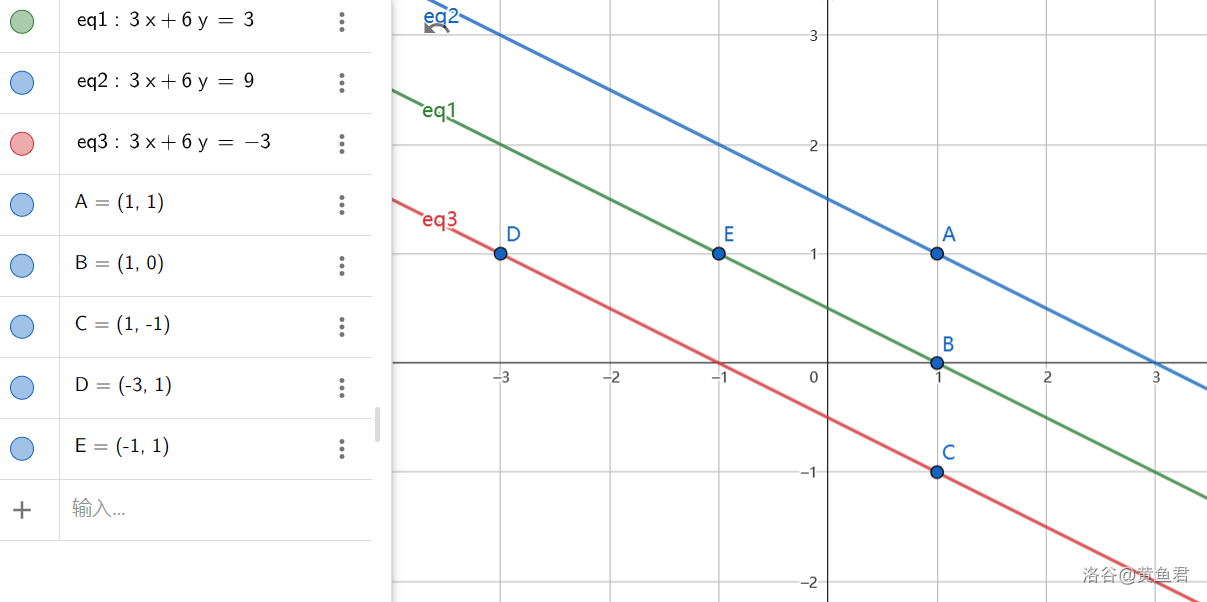
我们不妨画出直线$ax+by=c$

---

Q：不符合裴蜀定理的情况——与整数格点无交点

---

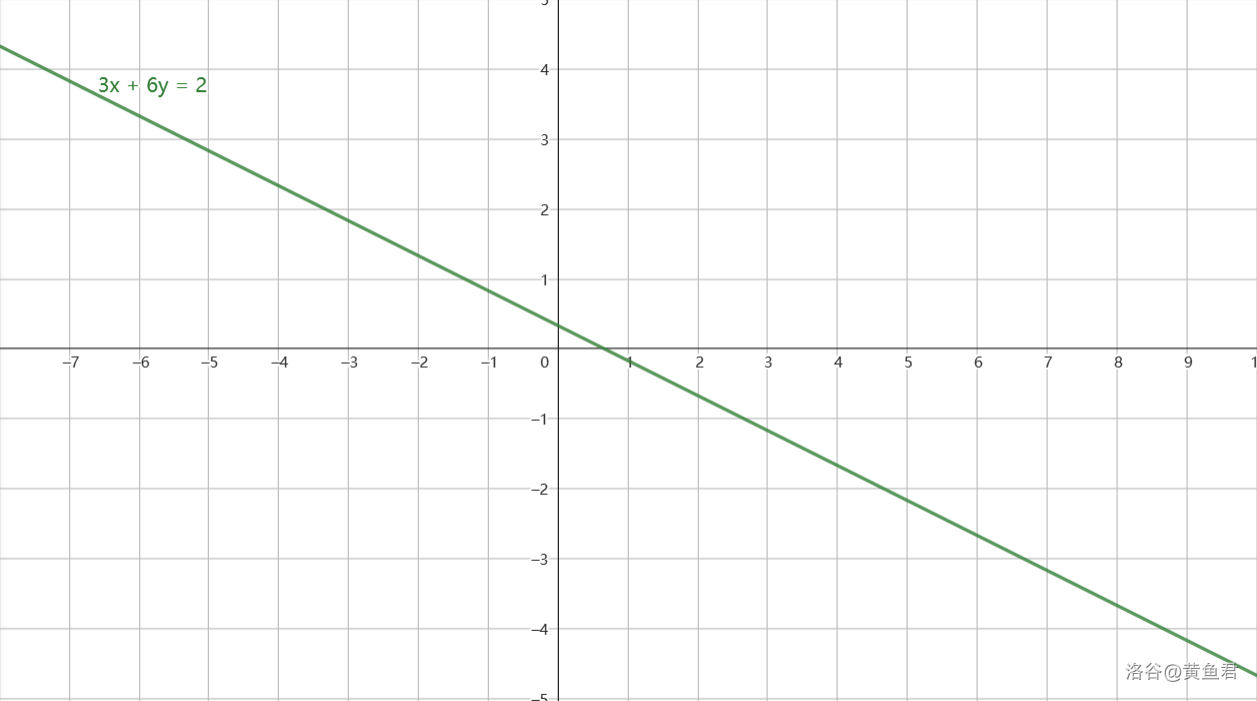
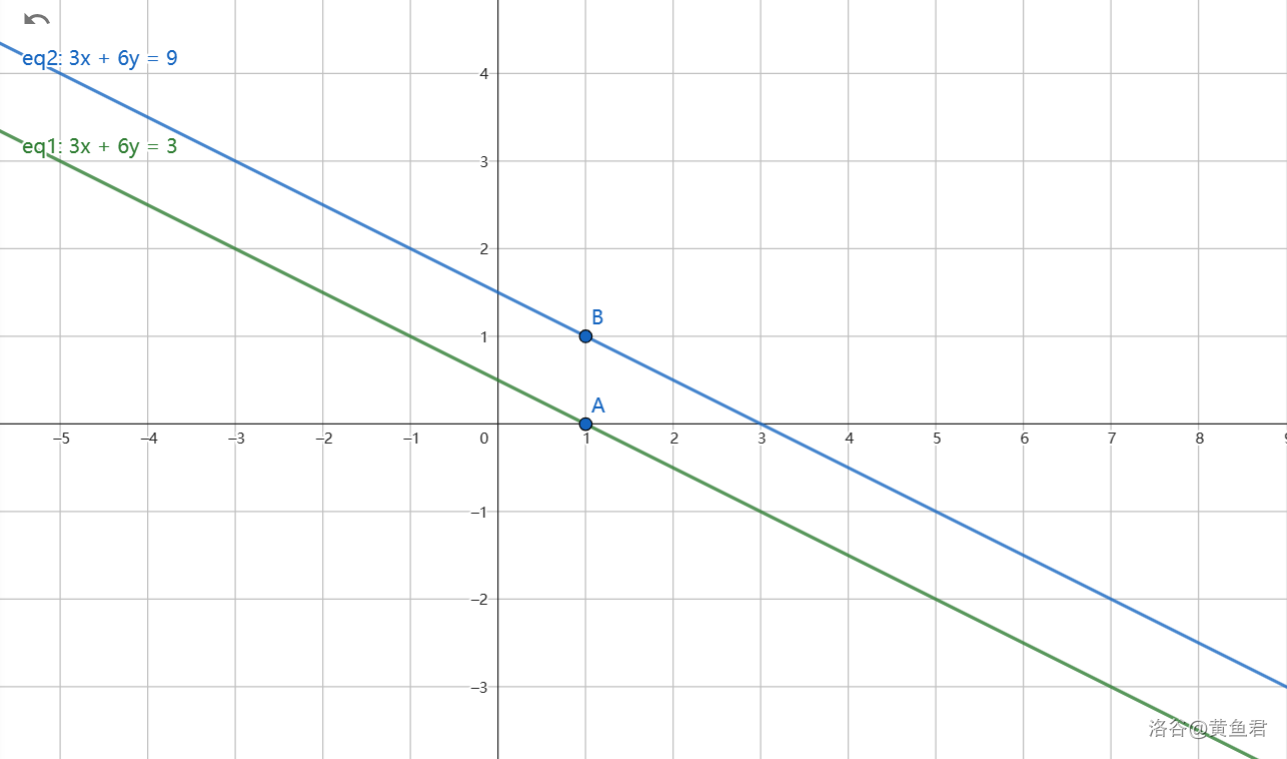
Q：为什么模数偏偏是$b/gcd,a/gcd$？

eq2为原方程，eq1为exgcd所求的方程，可以发现，eq1取(1,0)，乘倍数3后并不是x为最小整数解的点。

并且可以观察到，转化前后直线斜率相同，斜率三角形相同，故一旦确定一个格点$(x_0,y_0)$，则每一个解的$x,y$坐标在直线上挪动的距离也相同，所以模数也相同。

---

Q：$(x,y)$是否都能取正整数？

我们可以先算出$x$的最小正整数解，验证对应的$y$是否大于0；如小于0，则再算$y$的最小正整数，求出对应的$x$是否大于0（一定要二次确认，会存在$y>0$而$x$不是最小正整数解的情况）

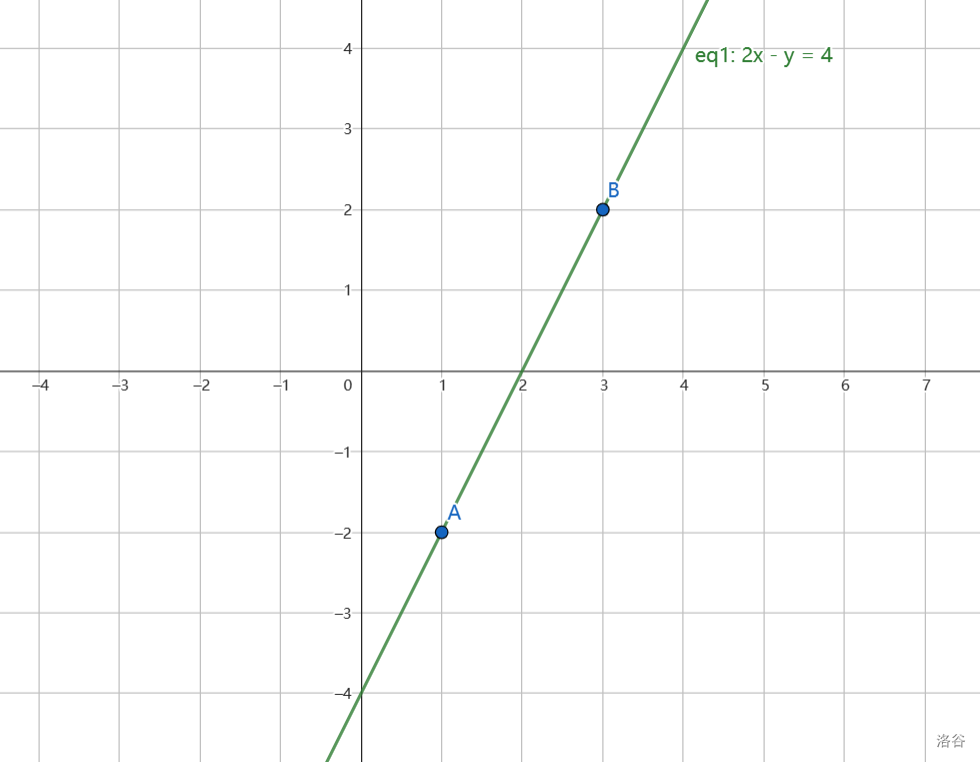
（下面这两幅图配的不太对） 凑合着看看，建议手画理解一下。